EXERCICE 1

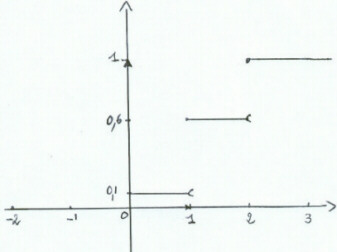
  1) a) La fonction de répartition de la variable aléatoire X est définie par : pour tout réel x ; F(x) = p(X £ x) soit :

x < 0 , F(x) = 0
x appartient à  [0 ; 1[ , F(x) = 0,1
x appartient à  [1 ; 2[ , F(x) = 0,6
x est supérieur ou égal 2 , F(x) = 1

Représentation graphique

 

b) E(X) = 0 x 0,1 + 1 x 0,5 + 2 x 0,4 = 1,3

2) a) p(C₁ Ç E) = p(E/C₁) x p(C₁) soit p(C Ç E) = 0,7 x 0,5 = 0,35

b) p(E/C2) = (0,7 x 0,3) + (0,7 x 0,3) soit p(E/C₂) = 0,42

Nous avons p(E/C₂) = p(E Ç C₂) / p(C₂) soit p(E/C₂) x p(C₂) = p(E Ç C₂) d'où p(E Ç C₂) = 0,42 x 0,4 = 0,168

c) p(E) = 0,35 + 0,168 = 0,518
 

3) p(Y = 1) = p(E) = 0,518 ;

p(Y = 2) = p(que 2 clients achètent de l'essence quand C₂ est réalisé) d'où p(Y = 2) = p(C₂) x P(Y = 2/C₂)
p(Y=2)= (0,7 x 0,7) x 0,4

p(Y = 0) = 1 -(0,518+0,193) = 0,286

EXERCICE 2

Avec z différent de 1 on a z - 2 = z² - z ce qui équivaut à z² - 2z + 2 = 0 soit (z - 1)² = i² qui admet 1 + i et 1 - i comme solutions. Avec z différent de 1 on a S = {1 + i ; 1 - i}.
On peut écrire 1 + i = donc 1 + i a pour module et pour argument p /4 ; 1 - i étant le conjugué de
1 + i    il aura même module et argument opposé - p /4.

2) Avec z différent de 1 on a : z - 2 = i .(z - 1) soit

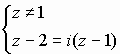
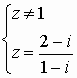
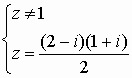
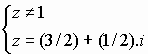
Conclusion : S₂ = {(3/2) + (1/2).i)}
 

 3) a) 

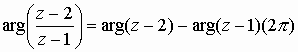
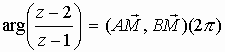
 b)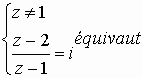 

M appartient à la médiatrice de [AB] (car MA = MB), son abscisse est 3/2 par conséquent. M appartient aussi au demi cercle de diamètre [AB] situé au dessus de l'axe des abscisses car l'angle est p /2.

D'où M a pour ordonnée 1/2 et l'affixe de M est 3/2 + 1/2 i.

4) a) Si z vérifie 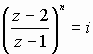alors 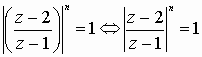soit 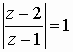de ce fait 

M appartient à la médiatrice de [AB] et admet pour abscisse 3/2.
 
 

b) Compte tenu de la question précédente, toute solution de l'équation 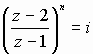est de la forme 3/2 + y.i où y est un réel.

Déterminons y :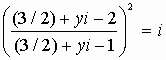 si et seulement si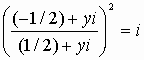 

(-1/2 + yi)² = i(1/2 + yi)²

1/4 - y² - yi = i(1/4 - y² + yi)

0 = y² - y - 1/4 + i(1/4 - y² + y) or un nombre complexe est nul si et seulement si sa partie réelle et sa partie imaginaire sont nulles toutes les deux. (Rappel : y est réel) d' où y² - y -1/4 = 0 et -y² + y + 1/4 = 0 soit y² -y - 1/4 = 0

On résoud une équation du second degré dans IR, on trouve le discriminant et deux solutions

      ou 

Les solutions dans l'ensemble des nombres complexes sont donc :

     et 
 
 

PROBLEME

PARTIE A

1) h est la différence de 2 fonctions dérivables sur IR⁺, donc h est dérivable sur IR⁺ et pour tout x de IR⁺ on a

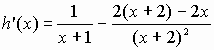
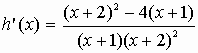
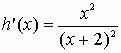
Pour tout x de IR⁺, h'(x)>0 et h'(0)=0, h est strictement croissante sur IR⁺ privé de 0 et h(0) = 0 donc h est strictement croissante sur IR⁺.

2) h est strictement croissante sur IR⁺ avec h(0) = 0 donc nous avons : pour tout x de IR⁺ privé de 0, h(x) > 0, f(x) > g(x).

d'où pour tout x positif ou nul :

3) La courbe représentative de la fonction f se déduit de celle de la fonction ln (connue) par une translation de vecteur .La fonction g est une fonction homographique dont la dérivée est donnée, pour tout x de IR⁺, par g'(x) = 4 / (x+2)² , elle est donc strictement croissante sur cet intervalle.

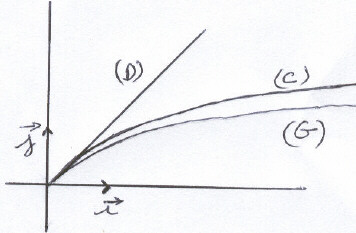
Représentation de f et g : (NB : f '(0) = g'(0) donc même tangente à l'origine)

PARTIE B

  1) f₁ étant la différence de 2 fonctions dérivables sur IR+, elle est elle même dérivable sur cet intervalle : on a

f₁ est strictement décroissante sur IR⁺.

2) Pour tout x > 0,

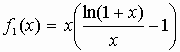et limite (quand x tend vers + l'infini) de f₁(x) vaut donc moins l'infini.

f₁(0) = 0.

3) La fonction f₁ est dérivable et strictement décroissante sur IR⁺ privé de 0 avec f₁(0) = 0. Nous pouvons en déduire que, pour tout x de IR⁺, f₁(x) £ 0, soit encore sur ce même intervalle : ln(1+x) - x £ 0.
D'où ln(1+x) £ x

4) Pour tout x ³ 0et pour tout k ³ 1, x £ kx. Nous pouvons en conclure que : si k ³ 1alors, pour tout x ³ 0, f(x) £ 0.

5) Pour 0 < k < 1 et x positif ou nul ,

donc la dérivée de f_k s'annule pour 

D'où : f_k'(x) > 0 pour 

f_k'(x) < 0 pour 

f_k'(x) = 0 pour x = (1-k) / k

f_k est strictement croissante sur [0;(1-k) / k] et strictement décroissante pour x supérieur ou égal à (1-k) / k dans IR.

6) Par conséquent, les valeurs de k >0, telles que, pour tout x supérieur ou égal à 0, f(x) £ kx sont les valeurs de k > 0 telles que, pour tout x supérieur ou égal à 0, f_k(x) £ 0 ( pour k supérieur ou égal à 1).
 
 

PARTIE C :

1) Calculons I à l'aide d'une intégration par parties en posant u(x) = ln(1+x) et v'(x) = 1. On a u'(x) = 1 / (1+x) et v(x) = x

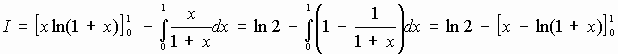
donc I = ln2 -1 + ln2 = 2ln2 - 1.

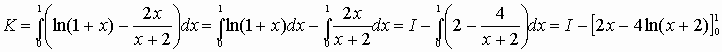
K = -1 + 2 ln2 -(2 - 4 ln3) + (-4 ln2) = -3 -2 ln2 + 4 ln3

Les intégrales J et K représentent, en unités d'aires, l'aire des portions de plan comprises entre la droite (D) et la courbe représentative de f (avec (D) au dessus de (C)) et les courbes (C) et (G) (avec (C) au-dessus de (G)). (voir schéma en partie A).

2)

D'après les résultats obtenus en partie A et B, nous pouvons écrire:

Pour x positif ou nul,         et pour x > 0 

Du 2 a) et b) , il s'ensuit qu'on peut écrire :

2 ln3 - 2 ln2 £ L £ 0,81 soit L = 0,9 à 10^-2 près